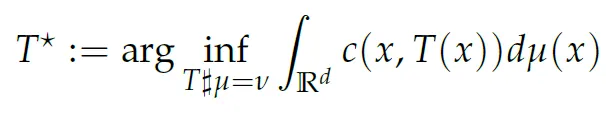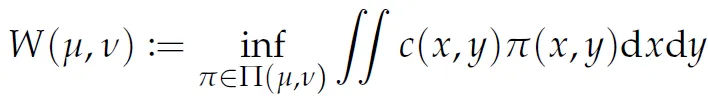Learning Single-Cell Perturbation Responses using Neural Optimal Transport

Tags
Single-cell modleing
Affiliation
ETH
Article type
Research
Date
2023/09/28
Journal
Nature Methods
Published Year
2023
keywords
Drug response prediction
Preprint version
Published version
Code
Seminar: Optimal Transport Modeling of Population Dynamics
CellOT_review.pptx
7268.7KB
Idea
•
Optimal transport with attention
•
Attention + gumbel softmax → RL
•
Optimal-transport flows for trajectory inference
arxiv.org
https://arxiv.org/pdf/2206.14928.pdf

Background

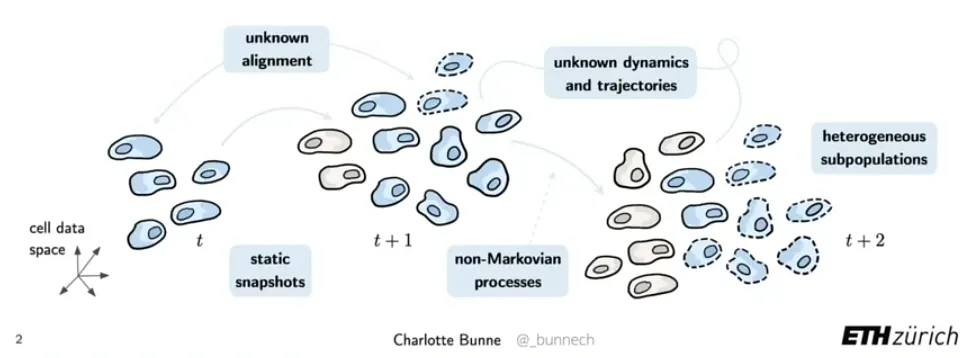
Dynamic process in single-cell biology

•
Given perturbation (e.g. drug administration)
◦
scRNA-seq can capture snapshot sampled from continuous-time trajectories of dynamic system.
◦
Cellular responses are heterogeneous, thus nedd to model cell dyanmics in single-cell level.

Optimal transport theory

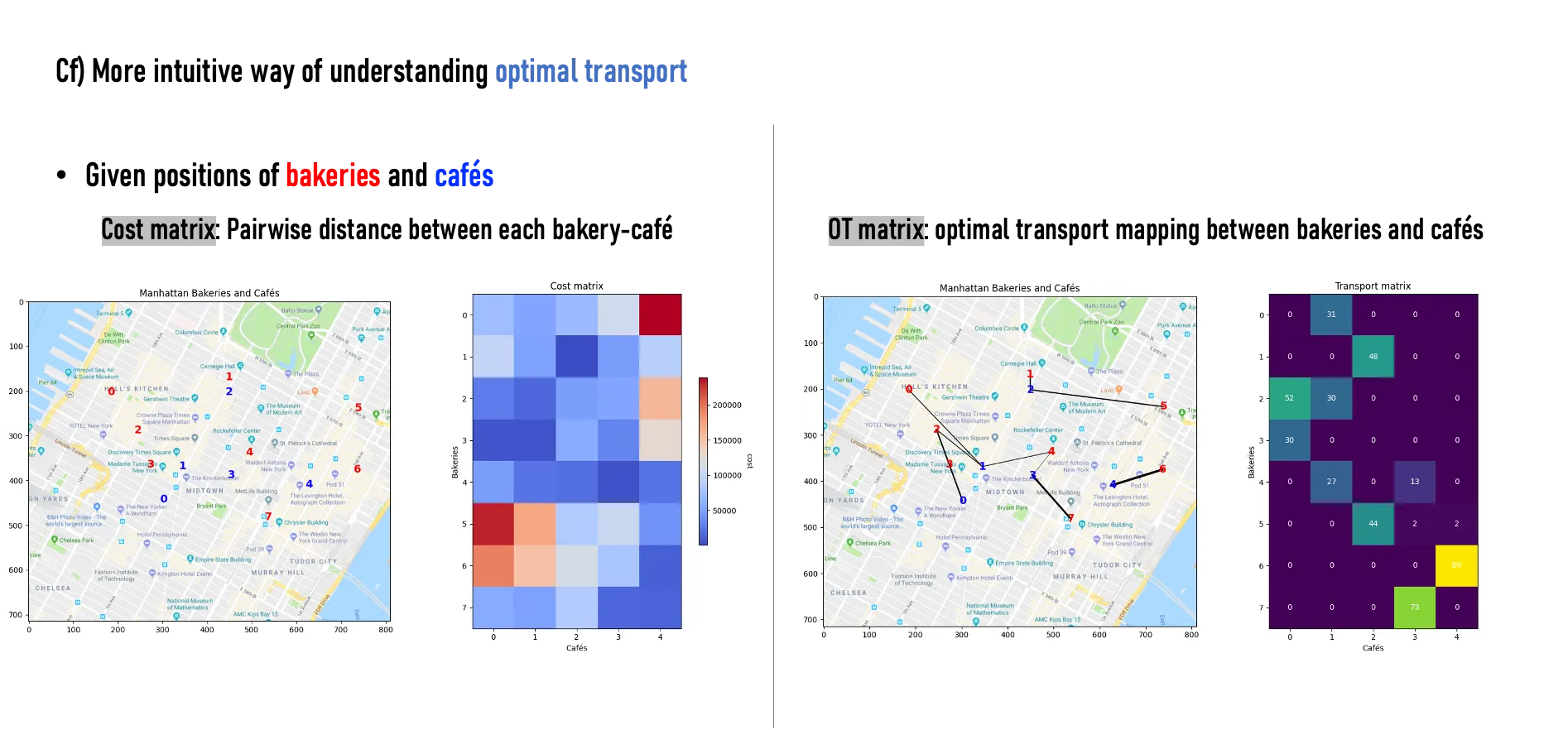
Q. Given two quantities of mass located at two different sites, what is the most efficient way to transport one into the other? A. Find a map T that pushes one mass onto the other in a way that minimizes the total cost of transport

Static OT (i.e. Monge map)

•
Given that two probability measure, μ,ν∈P(Rd)\mu, \nu \in P(\mathbb{R}^d) , find a map TT that pushes one mass onto the other in a way that minimizes the total cost of transport

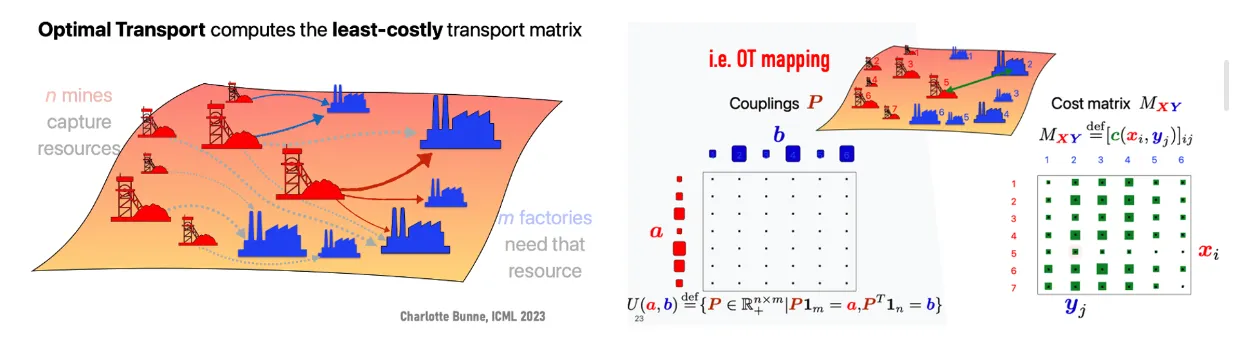
Kantorovich Relaxation

•
Relaxation to non-convex and difficult-to-solve Monge problem
•
Probabilistic correspondences that allow for the transportation of mass from a single source point to various target points (mass splitting)

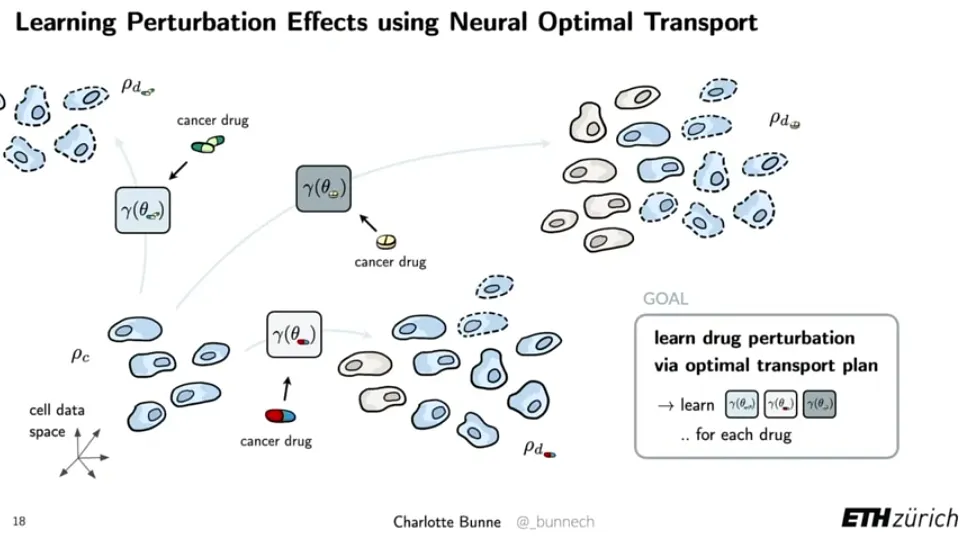
Task (in ML perspective)

•
Distribution matching for learning dynamics in perturbation effects i.e. Morph a data distribution to another data distribution of interest

Challenges

•
Traditional OT methods do not enable out-of-sample predictions on unseen cells and forecasting of cellular dynamics

Methods

•
Dataset
◦
SciPlex 3 [2020, Science]
▪
control setting vs. treated setting for all cancer drugs
▪
effects of 188 compounds in three cancer lines
◦
patients with lupus
▪
response of eight patients with lupus to interferon (IFN)-β
◦
patients with glioblastoma
▪
seven glioblastoma patients are measured in an untreated and Panobinostat-treated state
•
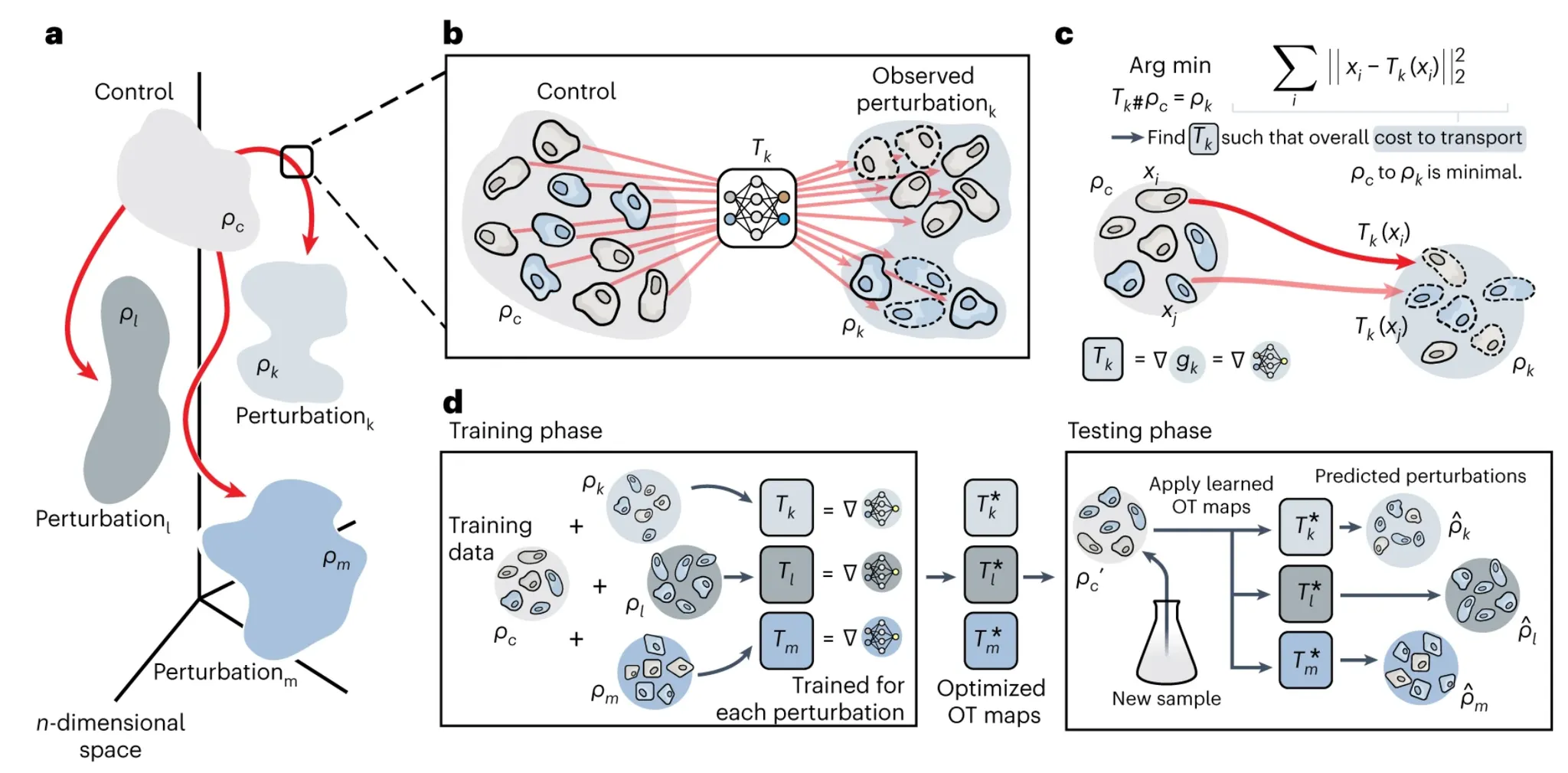
Method
◦
Training
▪
input : Cell state observation of unperturbed vs perturbed condition
▪
output : Trained transport plan TkT_k
◦
Testing
▪
input : Cell state observation of unperturbed condition
▪
output : Cell state observation of perturbed condition
◦
Detailed method
Optimal Transport problem as neural network

Results

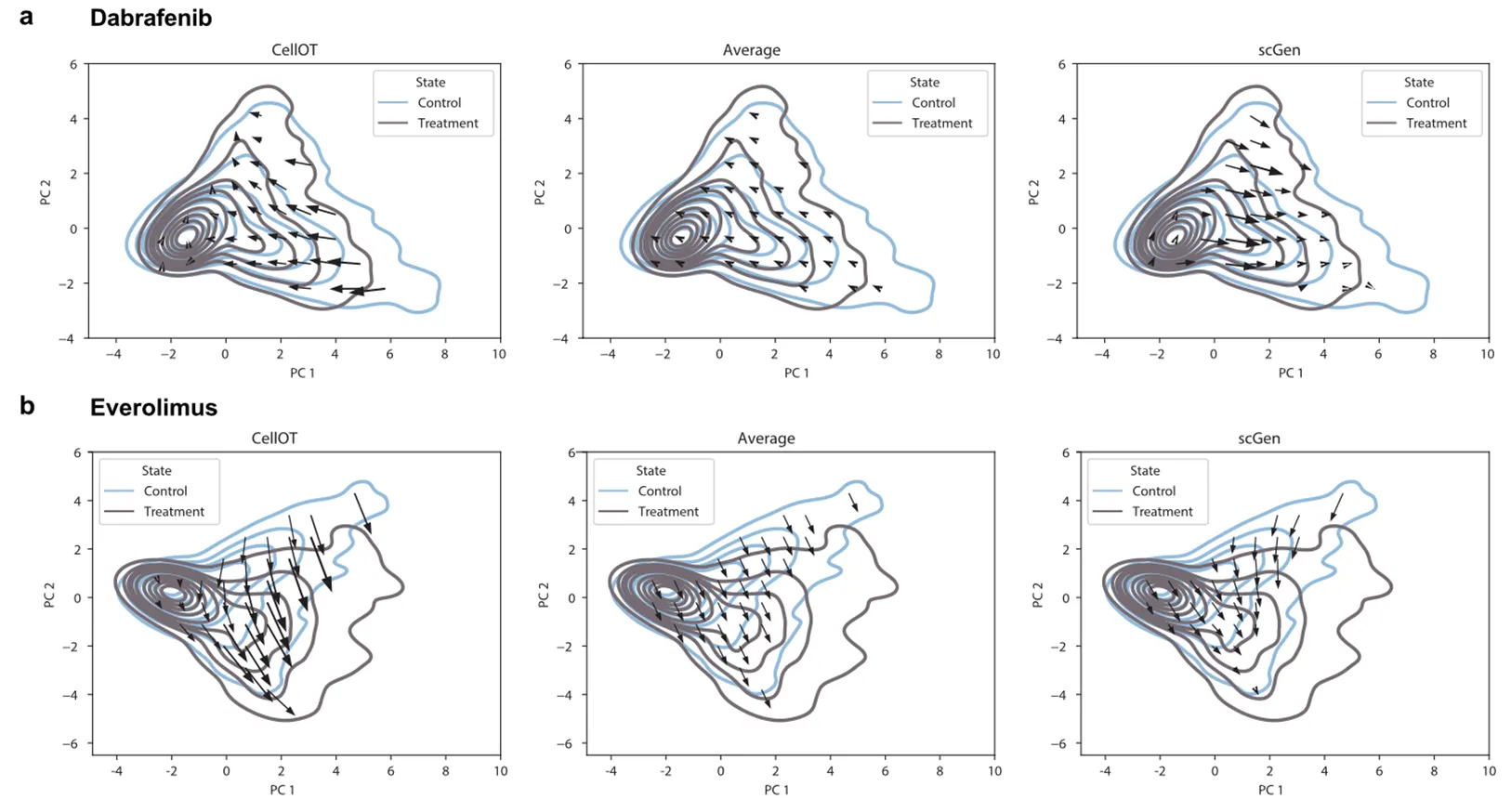
CellOT facilitates the multiplexed single-cell characterization of cancer drugs

CellOT generalizes to unseen patients and cell subpopulations.

f∗(y)=max⁡xyTx−f(x)f^{∗}(y) = \max_x y^Tx−f(x)

Implementation

Q. 왜 scRNA-seq count 데이터인데 negative value가 있지? Preprocessing을 어떻게 했길래?
Q. How cell state dist. is implemented?
Q. What is model trained in cellOT?
Q. Configuration setting